שיעור - וקטורים: תיאור מישור

לצפיה נצפה לצפיה חוזרת

תוכן השיעור

הדרכים לקביעת מישור במרחב:

(1)דרך שלוש נקודות שאינן על ישר אחד עובר מישור אחד ויחיד.
(2)דרך שני ישרים נחתכים עובר מישור אחד ויחיד.
(3)דרך ישר ונקודה שמחוץ לישר עובר מישור אחד ויחיד.
(4)דרך שני ישרים מקבילים עובר מישור אחד ויחיד.
 

 

 

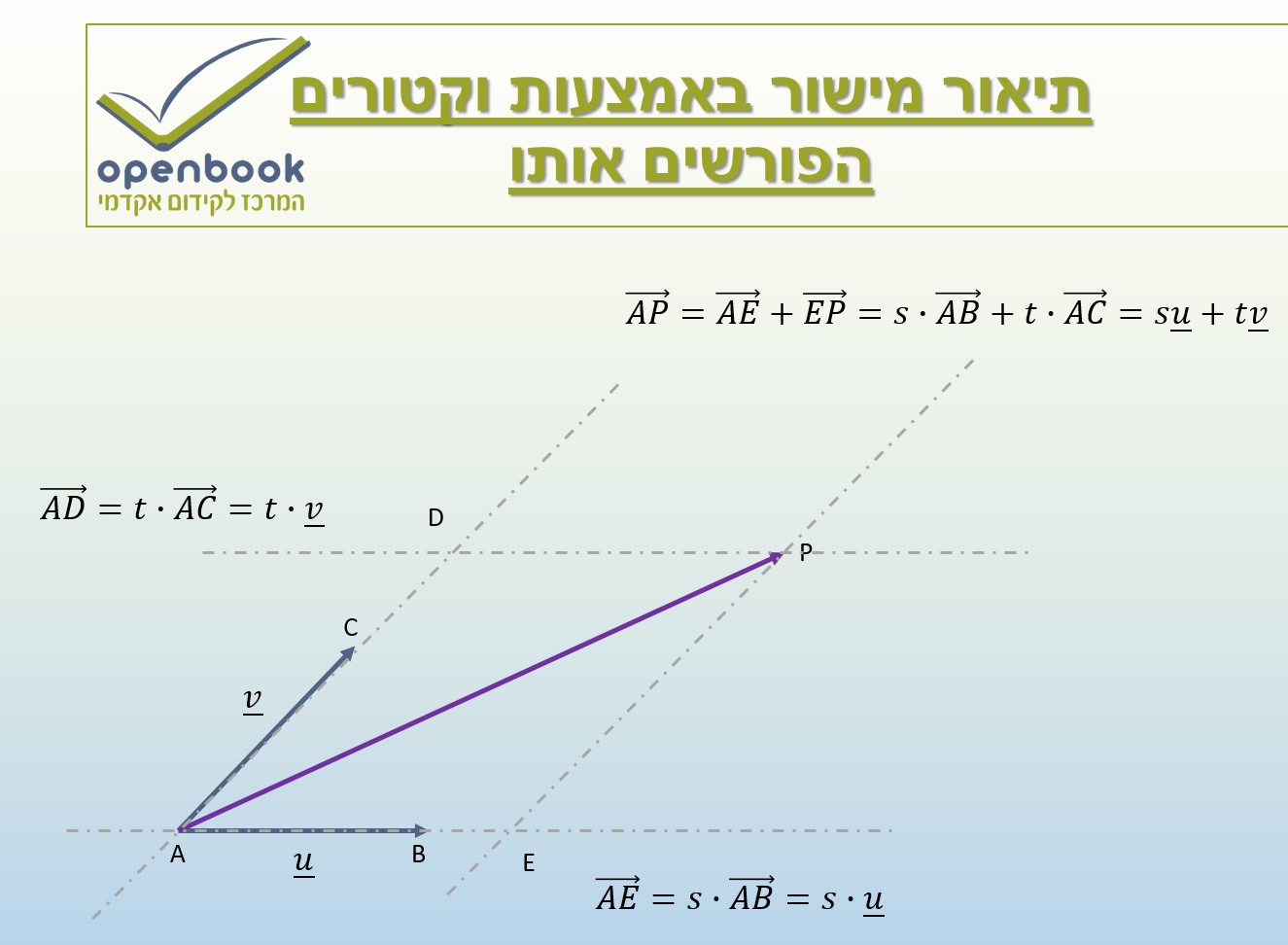
תיאור של מישור

 

שני ווקטורים בעלי מוצא משותף שאינם על ישר אחד קובעים מישור אחד ויחיד.

כל וקטור במישור הוא קומבינציה(צירוף) לינארית של הווקטורים הפורשים אותו.

למעשה, מכאן נובע שנקודה כלשהי במרחב תימצא על מישורABC  אם ניתן להגיע אליה באמצעות קומבינציה לינארית של ▁u ו- ▁v. 

תרגיל וקטור המקביל למישור

 

וקטור מקביל למישור כאשר הוא ניתן להצגה באמצעות שני הווקטורים הפורשים את המישור בלבד , והוא יוצא מנקודה שאינה נמצאת על המישור 

נתון הווקטור: ▁u+1/3 ▁v+(t-1/4) ▁w

מצא עבור איזה ערך של t, הווקטור מקביל למישור הנפרש על ידי שני הווקטורים ▁u ו- ▁v.

 

התנאי שהנקודה נמצאת בתוך המשולש
(קביעת מיקומה של הנקודה במשולש)

 

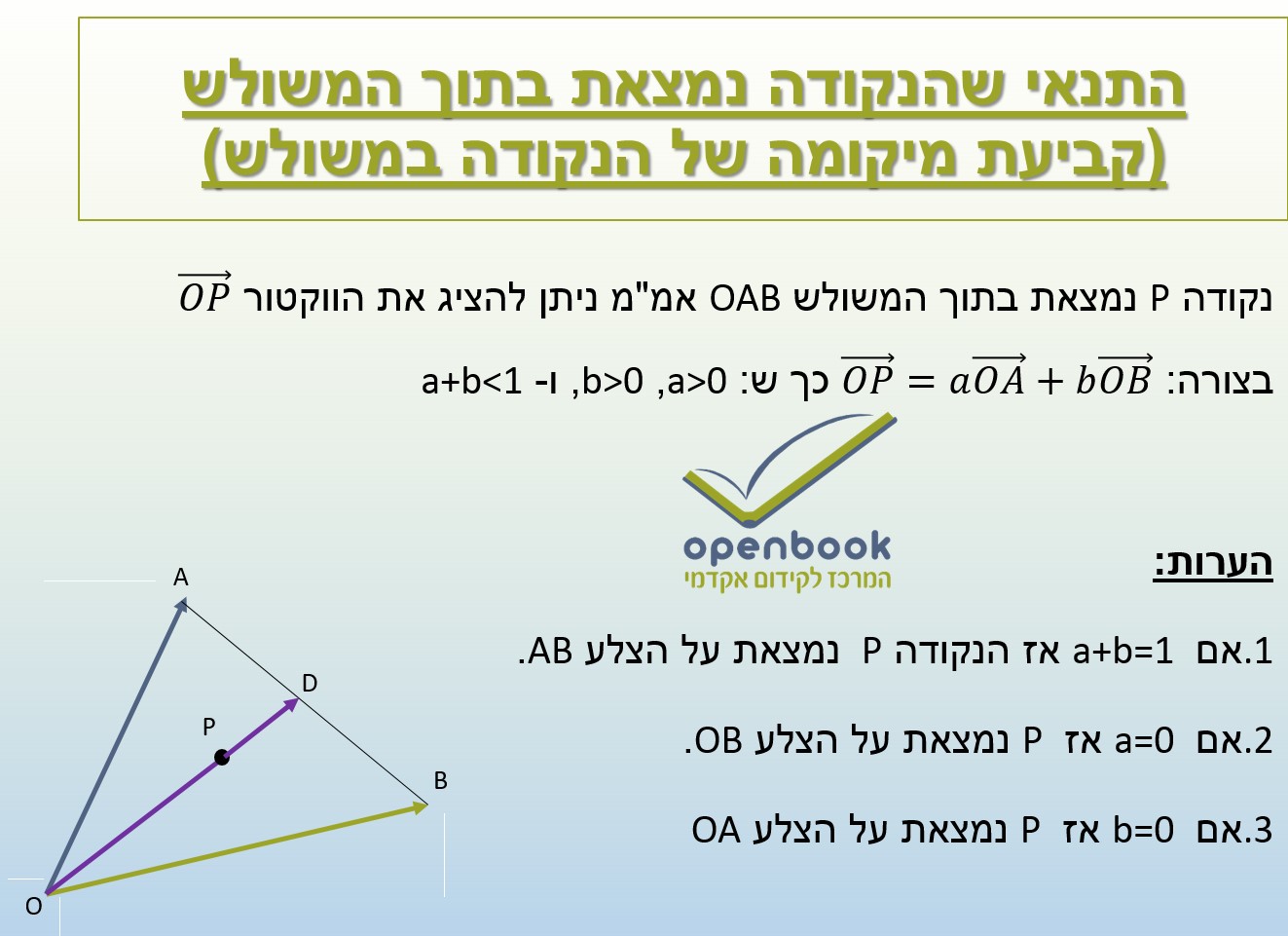
נקודה P נמצאת בתוך המשולש OAB אמ"מ ניתן להציג את הווקטור (OP) ⃗    בצורה: (OP) ⃗=a(OA) ⃗+b(OB) ⃗ כך ש: a>0, b>0, ו- a+b<1

 

הערות:

.1אם a+b=1  אז הנקודה P  נמצאת על הצלע AB.
.2אם a=0  אז P  נמצאת על הצלע OB.
.3אם b=0  אז P  נמצאת על הצלע OA

 

 

 

 

שאלות ותשובות

יש לך שאלה?
נשמח לענות! נפרסם את שאלתך והתשובה כדי לסייע לאחרים
לרשום שאלה

סרטונים נוספים

00:13:17