שיעור - וקטורים חלק ו' תלות ליניארית בין שני וקטורים, תיאור של ישר, וקטורים שמוצאם באותה נקודה וסופם

לצפיה נצפה לצפיה חוזרת

תוכן השיעור

תלות ליניארית בין שני וקטורים

 

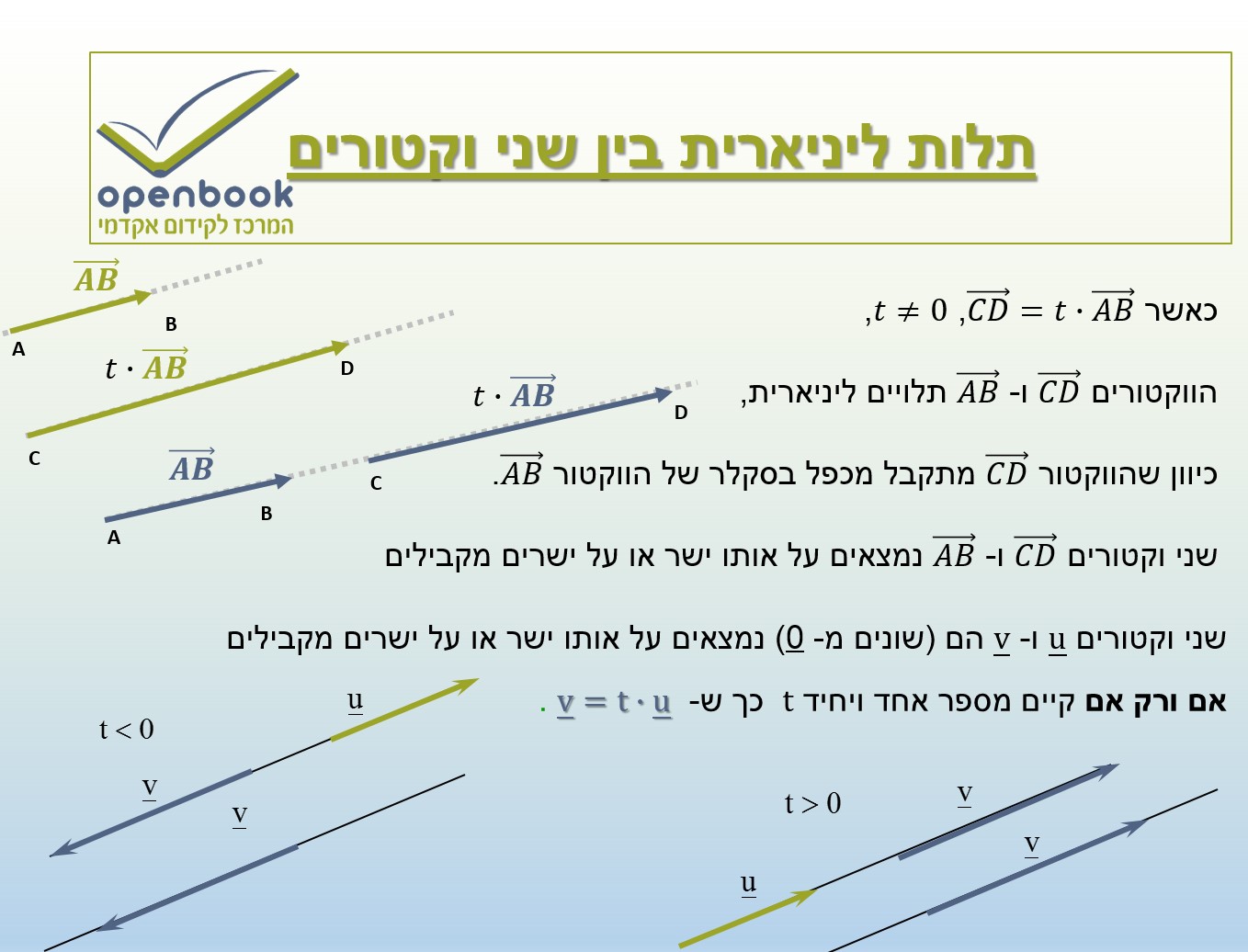
כאשר (CD) ⃗=t∙(AB) ⃗, t≠0,

הווקטורים (CD) ⃗ ו- (AB) ⃗ תלויים ליניארית,

כיוון שהווקטור (CD) ⃗ מתקבל מכפל בסקלר של הווקטור (AB) ⃗.

שני וקטורים (CD) ⃗ ו- (AB) ⃗ נמצאים על אותו ישר או על ישרים מקבילים

 

שני וקטורים ▁u ו- ▁v הם (שונים מ- 0) נמצאים על אותו ישר או על ישרים מקבילים

אם ורק אם קיים מספר אחד ויחיד t  כך ש-  ▁v=t∙▁u .

 

הווקטור הגיאומטרי- תיאור של ישר

 

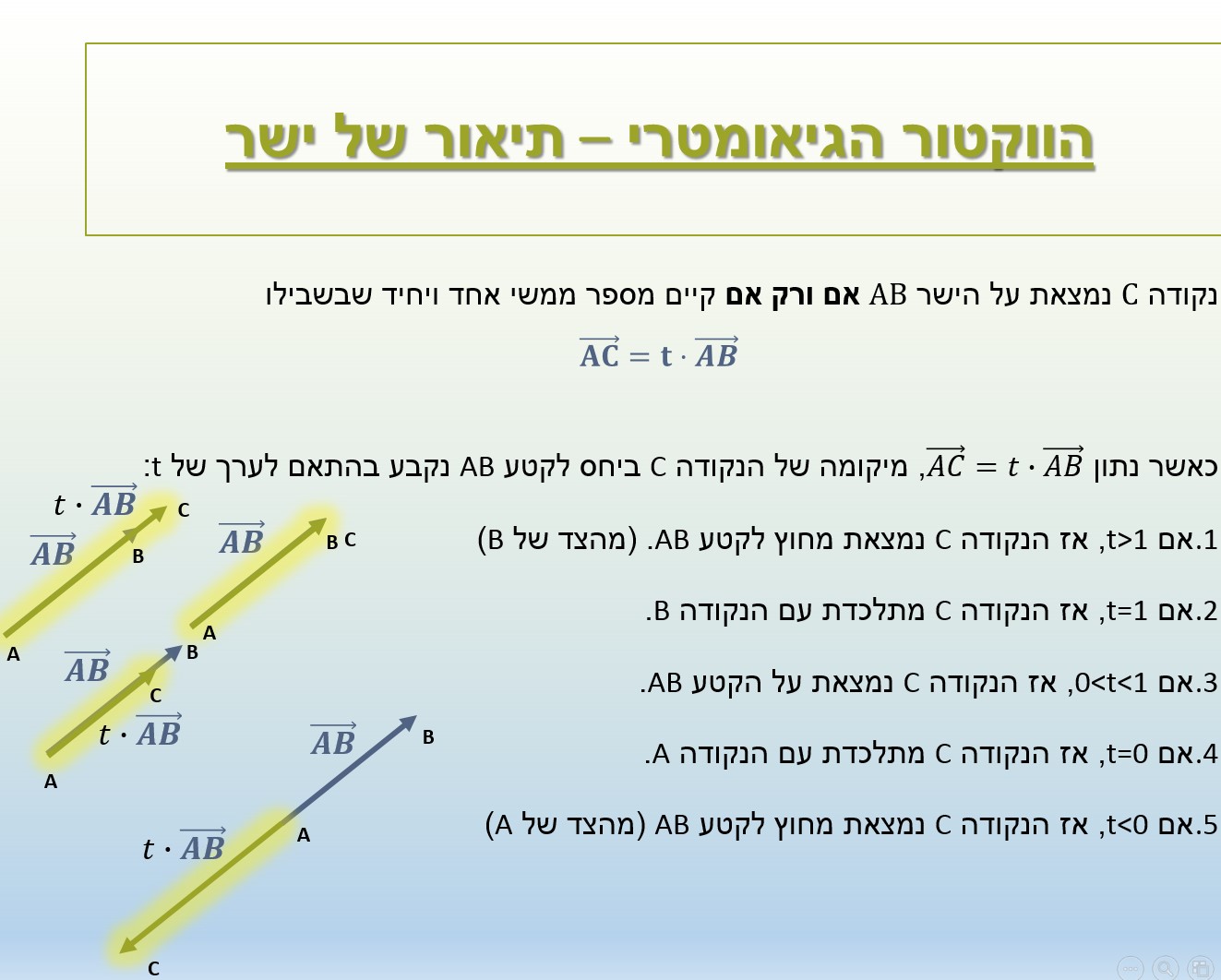
נקודה C נמצאת על הישר AB אם ורק אם קיים מספר ממשי אחד ויחיד שבשבילו

(AC) ⃗=t⋅(AB) ⃗

 

כאשר נתון (AC) ⃗=t∙(AB) ⃗, מיקומה של הנקודה C ביחס לקטע AB נקבע בהתאם לערך של t:

.1אם t>1, אז הנקודה C נמצאת מחוץ לקטע AB. (מהצד של B)
.2אם t=1, אז הנקודה C מתלכדת עם הנקודה B.
.3אם 0<t<1, אז הנקודה C נמצאת על הקטע AB.
.4אם t=0, אז הנקודה C מתלכדת עם הנקודה A.
.5אם t<0, אז הנקודה C נמצאת מחוץ לקטע AB (מהצד של A)
 
 

תרגיל

 

נתונים הוקטורים: (AB) ⃗=▁v  , (AC) ⃗=3▁v , (AD) ⃗=-1/8 ▁v

א. הסבר מדוע כל ארבע הנקודות A,B,C ו- D נמצאות על ישר אחד.

ב. קבע את סדר הנקודות A, B, C, ו-D על הישר AB

 

וקטורים שמוצאם באותה נקודה וסופם על אותו ישר

 

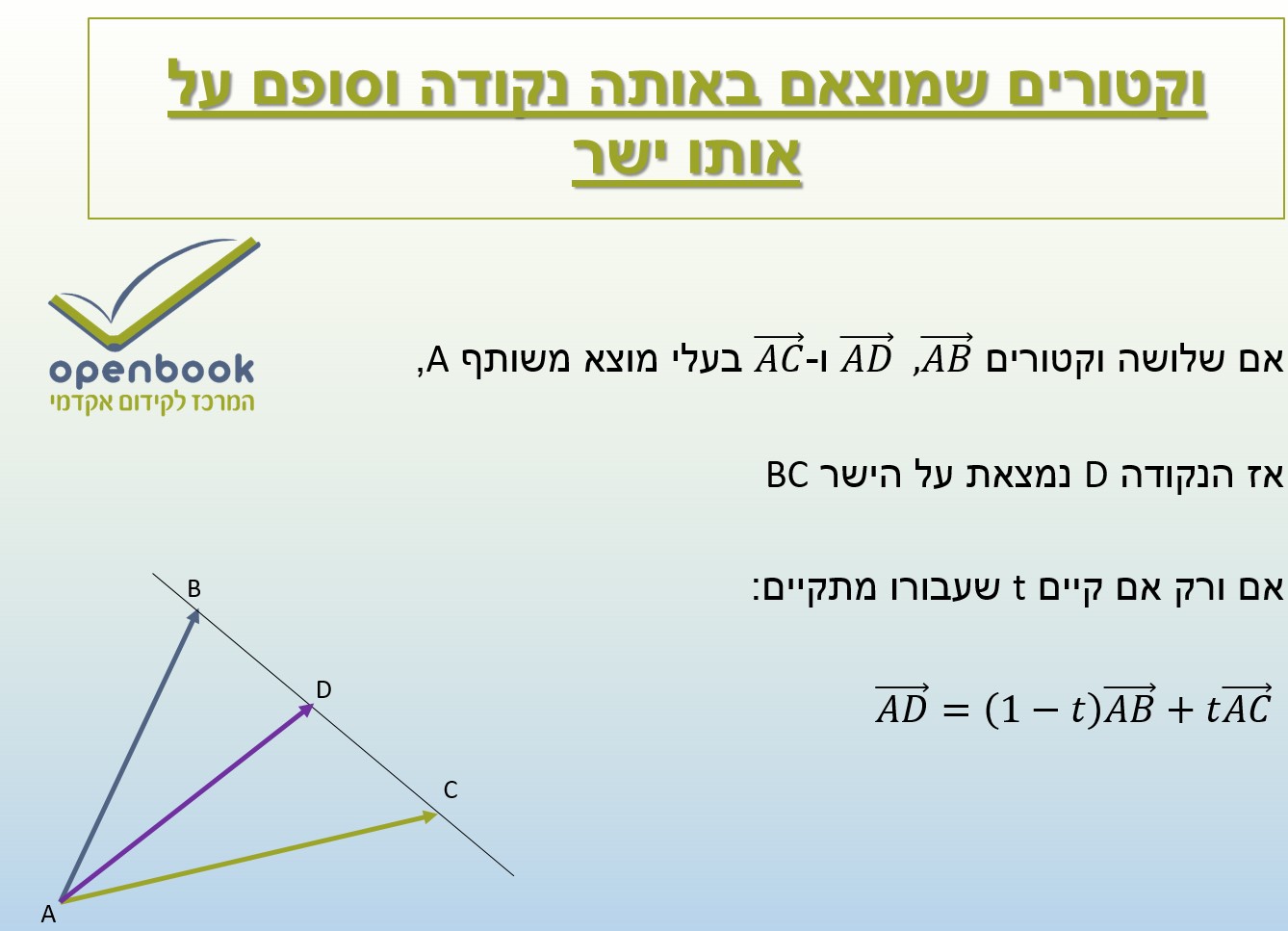
אם שלושה וקטורים (AD) ⃗   ,  (AB) ⃗ ו-(AC) ⃗ בעלי מוצא משותף A,

אז הנקודה D נמצאת על הישר BC

אם ורק אם קיים t שעבורו מתקיים:

 (AD) ⃗=(1-t) (AB) ⃗+t(AC) ⃗

 

חלוקת קטע ביחס נתון

 

 

כאשר הנקודה P נמצאת על הקטע AB מתקיים:

(AP) ⃗=t(AB) ⃗

(PB) ⃗=(1-t) (AB) ⃗

 

 

שאלות ותשובות

יש לך שאלה?
נשמח לענות! נפרסם את שאלתך והתשובה כדי לסייע לאחרים
לרשום שאלה

סרטונים נוספים

00:13:00