שיעור 7 - מספר ממשי ומרוכב במישור של גאוס וערך מוחלט

לצפיה נצפה לצפיה חוזרת

תוכן השיעור

מספר ממשי על ציר המספרים

 

 

כל המספרים הממשיים, צורתם  z=x+0·𝑖

כל מספר ממשי מתאימה הנקודה (x,0) על הציר האופקי שהוא ציר המספרים הממשיים.

לכן, ציר זה נקרא הציר הממשי.

 

מספר מדומה

 

כל המספרים המדומים צורתם z=0+y·𝑖

כל מספר מדומה מתאימה נקודה (0, y) על הציר האנכי.

לכן, ציר זה נקרא הציר המדומה.

 

הצגה גרפית של
מספר מרוכב באמצעות נקודה

 

לכל מספר מרוכב z=x+yi מותאמת נקודה יחידה ( x , y) ולהפך.

ציר ה- x ציר זה נקרא הציר הממשי

ציר ה-y ציר זה נקרא הציר המדומה

הצגה זו נקראת ההצגה הקרטזית או האלגברית של המספר המרוכב z=x+yi

המישור המיוצר ע"י מערכת הצירים הנ"ל נקרא המישור של גאוס

 

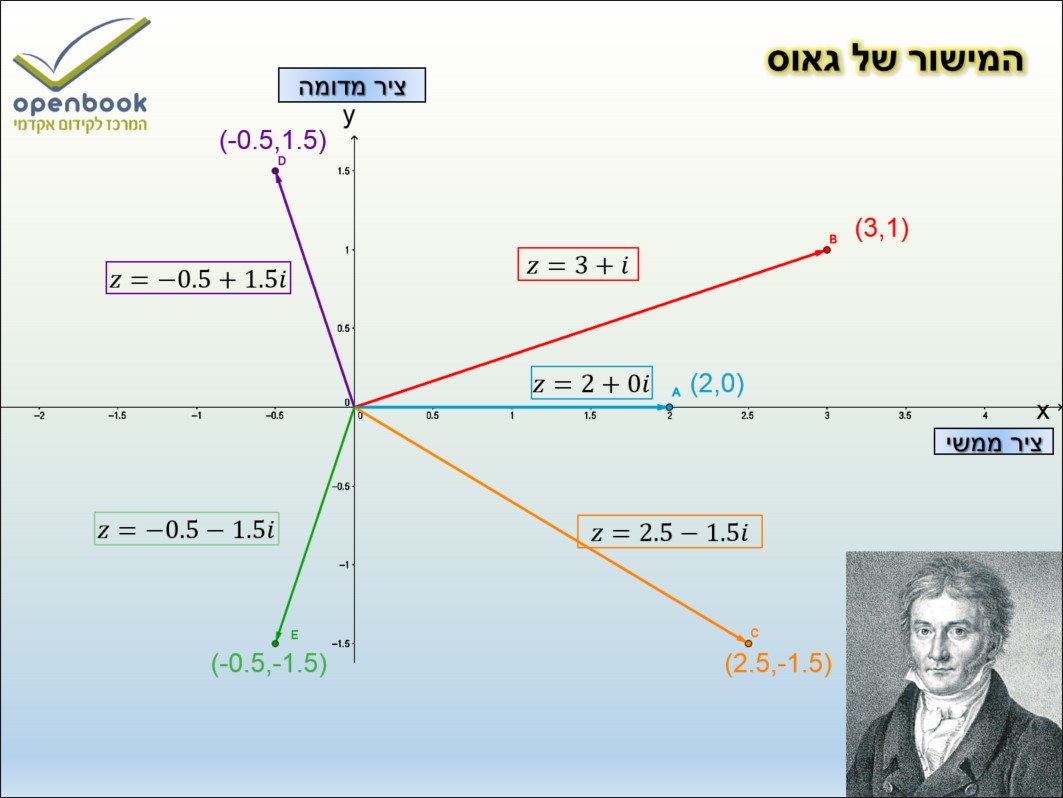
הערך המוחלט

 

כשעסקנו במספרים ממשיים, ראינו כי אם נתון מספר ממשי a, אז הערך המוחלט שלו מסומן: |a| ומייצג את מרחקה של הנקודה (a,0) מראשית הצירים.

נגדיר את הערך המוחלט של מספר מרוכב:

אם נתון מספר מרוכב בהצגתו האלגברית z=x+yi, אז הנקודה המתאימה לו במישור היא (x,y).

הערך המוחלט של z יסומן |z| מוגדר כמרחק הנקודה (x,y) מראשית הצירים.

לפי משפט פיתגורס או לפי הנוסחה למרחק בין שתי נקודות נקבל:

|z|=|x+yi|=√(x^2+y^2 )

 

 

שאלות ותשובות

יש לך שאלה?
נשמח לענות! נפרסם את שאלתך והתשובה כדי לסייע לאחרים
לרשום שאלה

סרטונים נוספים

00:06:00