חקירה: הקשר בין פונקציה לנגזרתה
🔍 חקירה: הקשר בין פונקציה לנגזרתה
🎯 מטרת הפעילות
בפעילות זו תגלו בעצמכם את הקשר המופלא בין גרף של פונקציה לגרף של הנגזרת שלה.
שאלת המפתח: אם אני יודע איך נראה גרף של פונקציה, האם אני יכול לצייר את גרף הנגזרת?
📚 תזכורת: מה זו נגזרת?
הנגזרת של פונקציה בנקודה מסוימת היא השיפוע של המשיק לגרף באותה נקודה.
$$f'(x_0) = \text{שיפוע המשיק לגרף } f \text{ בנקודה } x_0$$
🎮 חלק א': חקירה חופשית
📝 ענו על השאלות הבאות:
1. כאשר הנקודה נמצאת בחלק עולה של הפונקציה (הגרף הכחול), מה הסימן של השיפוע?
2. כאשר הנקודה נמצאת בחלק יורד של הפונקציה, מה הסימן של השיפוע?
3. כאשר הנקודה נמצאת בנקודת קיצון (מקסימום או מינימום), מה השיפוע?
🔮 חלק ב': הגילוי הגדול
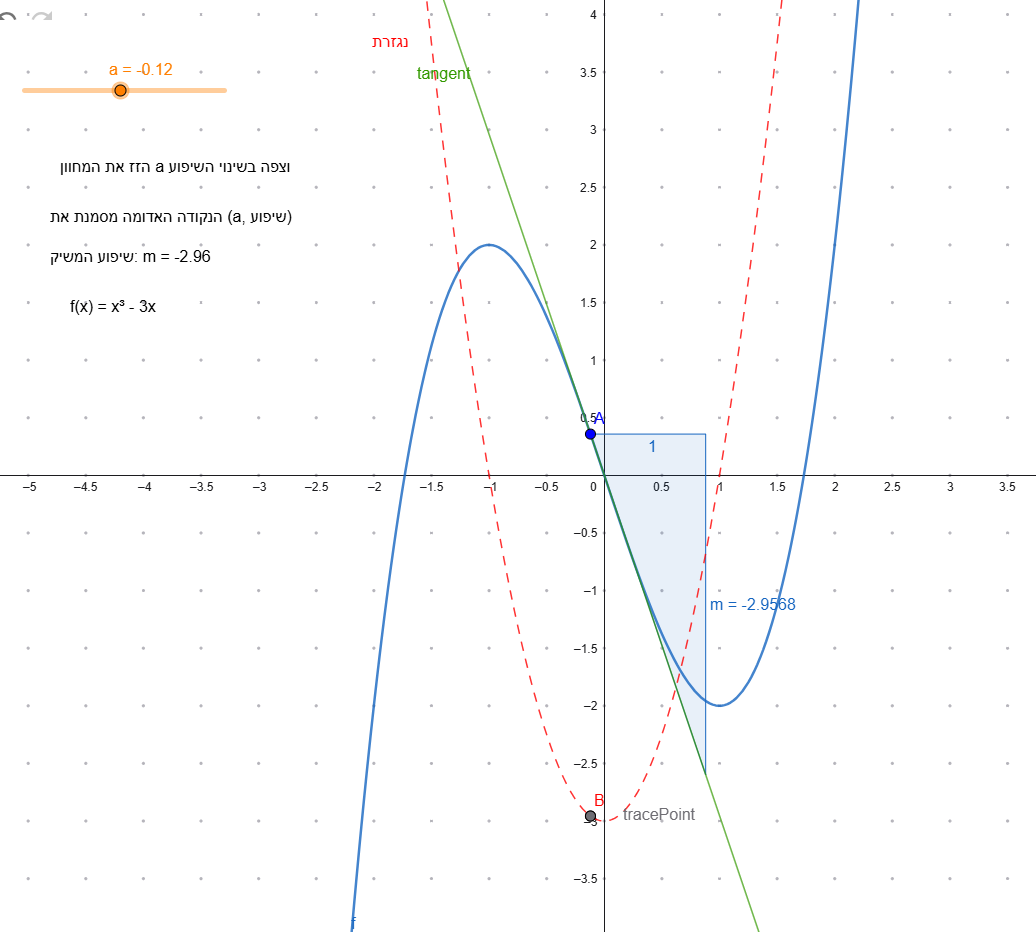
עכשיו נחשוף את גרף הנגזרת (הגרף האדום)!
לחצו על תיבת הסימון "הצג נגזרת" באפליקציה למעלה.
📝 השלימו את הטבלה:
הזיזו את הנקודה והשלימו:
| מצב הפונקציה f | סימן השיפוע | גרף הנגזרת f' נמצא... |
|---|---|---|
| f עולה ↗ | ______ | מעל / מתחת לציר x |
| f יורדת ↘ | ______ | מעל / מתחת לציר x |
| נקודת קיצון | ______ | ______ |
💡 חלק ג': סיכום והכללה
🏆 הכללים שגילינו:
✍️ חלק ד': תרגול
שאלה 1:
נתון גרף של פונקציה f. הפונקציה עולה בתחום $$(-\infty, 2)$$ ויורדת בתחום $$(2, \infty)$$.
א) מה סימן הנגזרת בתחום $$(-\infty, 2)$$? ______
ב) מה סימן הנגזרת בתחום $$(2, \infty)$$? ______
ג) מה ערך הנגזרת ב-$$x=2$$? ______
ד) מה סוג הנקודה $$x=2$$ בפונקציה f? ______
שאלה 2:
נתון ש-$$f'(x) > 0$$ לכל $$x < 1$$ וגם $$f'(x) < 0$$ לכל $$x > 1$$.
א) באילו תחומים הפונקציה f עולה? ______
ב) באילו תחומים הפונקציה f יורדת? ______
ג) מה קורה בנקודה $$x=1$$? ______
🎯 אתגר למתקדמים:
אם $$f(x) = x^3 - 3x$$, שרטטו (בערך) את גרף הנגזרת $$f'(x)$$ בלי לחשב!
רמז: מצאו איפה f עולה, איפה יורדת, ואיפה נקודות הקיצון.