פרבולה, משיק ואנכים

פרבולה, משיק ואנכים

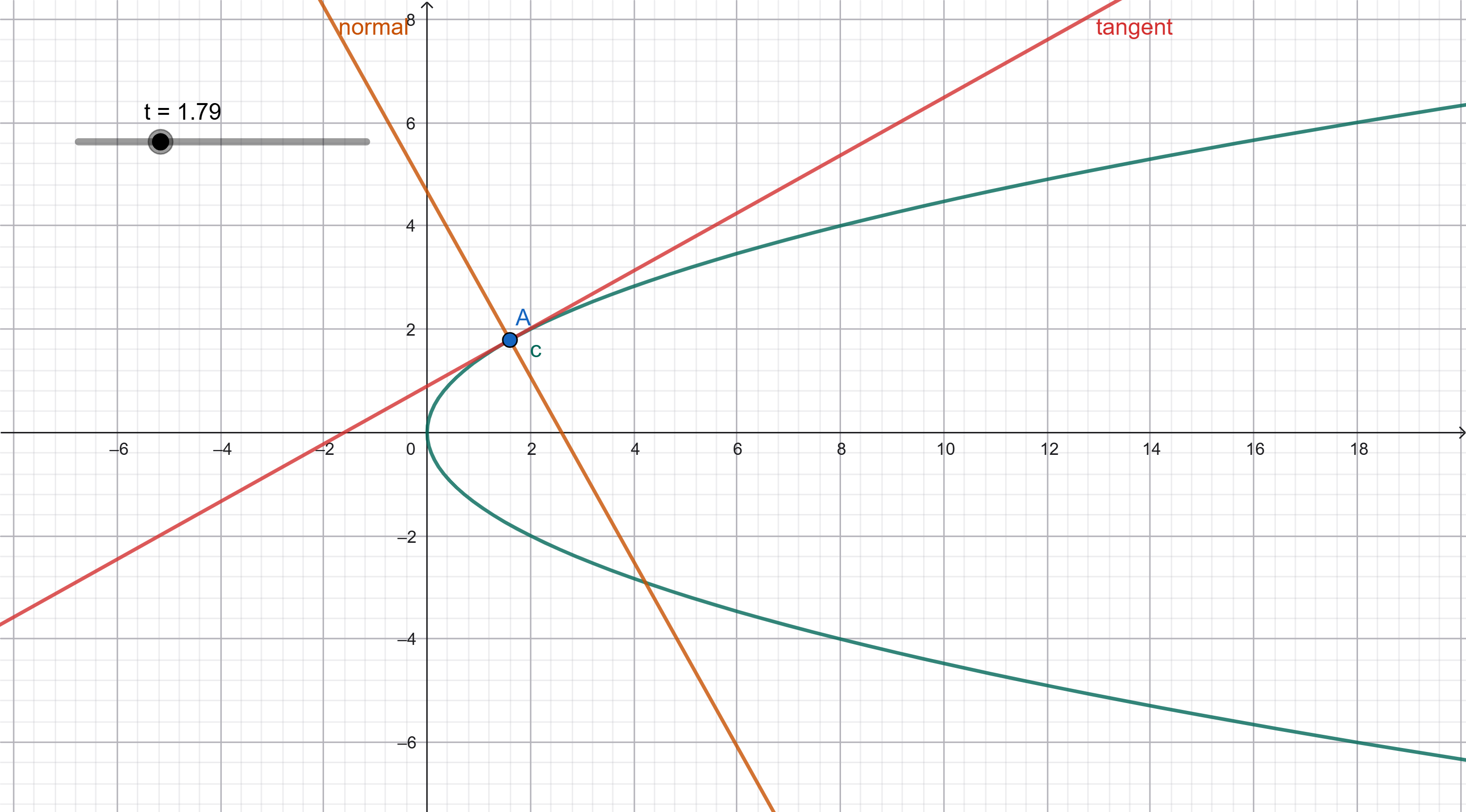
בדף זה נחקור את הקשרים בין פרבולה מהצורה \( y^2 = 2px \), לבין המשיק לפרבולה והאנך למשיק.

הפרבולה

המשוואה \( y^2 = 2px \) מגדירה פרבולה הפתוחה ימינה. נקודה \( (x_0 , y_0) \) נמצאת על הפרבולה אם ורק אם: \( y_0^2 = 2p x_0 \).

משיק לפרבולה

נוסחת המשיק בנקודה \( (x_0 , y_0) \) היא:

\( y y_0 = p(x + x_0) \)

שיפוע המשיק: \( m = \frac{p}{y_0} \).

האנך למשיק (Normal)

אם שיפוע המשיק הוא \( m \), אז שיפוע האנך הוא: \( -\frac{1}{m} \).

משוואת האנך בנקודה: \( y - y_0 = -\frac{1}{m}(x - x_0) \).

פעילות GeoGebra

גררו את הנקודה על הפרבולה ושימו לב כיצד המשיק והאנך משתנים.