חקירה: קעירות ונקודות פיתול
🔍 חקירה: קעירות ונקודות פיתול
הקשר בין הפונקציה, הנגזרת הראשונה והנגזרת השנייה
🎯 למה זה חשוב?
דמיינו שאתם נוהגים במכונית על כביש מפותל. השיפוע של הכביש אומר לכם אם אתם עולים או יורדים, אבל הקעירות אומרת לכם לאיזה כיוון ההגה פונה!
- קעור כלפי מעלה ∪ = ההגה פונה שמאלה (הכביש "מחבק" אתכם מלמטה)
- קעור כלפי מטה ∩ = ההגה פונה ימינה (הכביש "מחבק" אתכם מלמעלה)
- נקודת פיתול = הרגע שבו מחליפים כיוון פנייה!
📚 תזכורת: שלוש הפונקציות
💡 המפתח להבנה:
\(f''(x) > 0 \Rightarrow \text{קעור כלפי מעלה} \quad,\quad f''(x) < 0 \Rightarrow \text{קעור כלפי מטה}\)
🎮 חלק א': חקירה אינטראקטיבית
📋 הוראות הפעלה:
- בחרו פונקציה באמצעות המחוון העליון (1-5)
- הזיזו את המחוון a לאורך הגרף וצפו בשינויים
- סמנו את תיבות הסימון כדי לראות את f'(x) ו-f''(x)
- עיגול הקעירות מראה מאיזה צד הגרף "מתעקל"
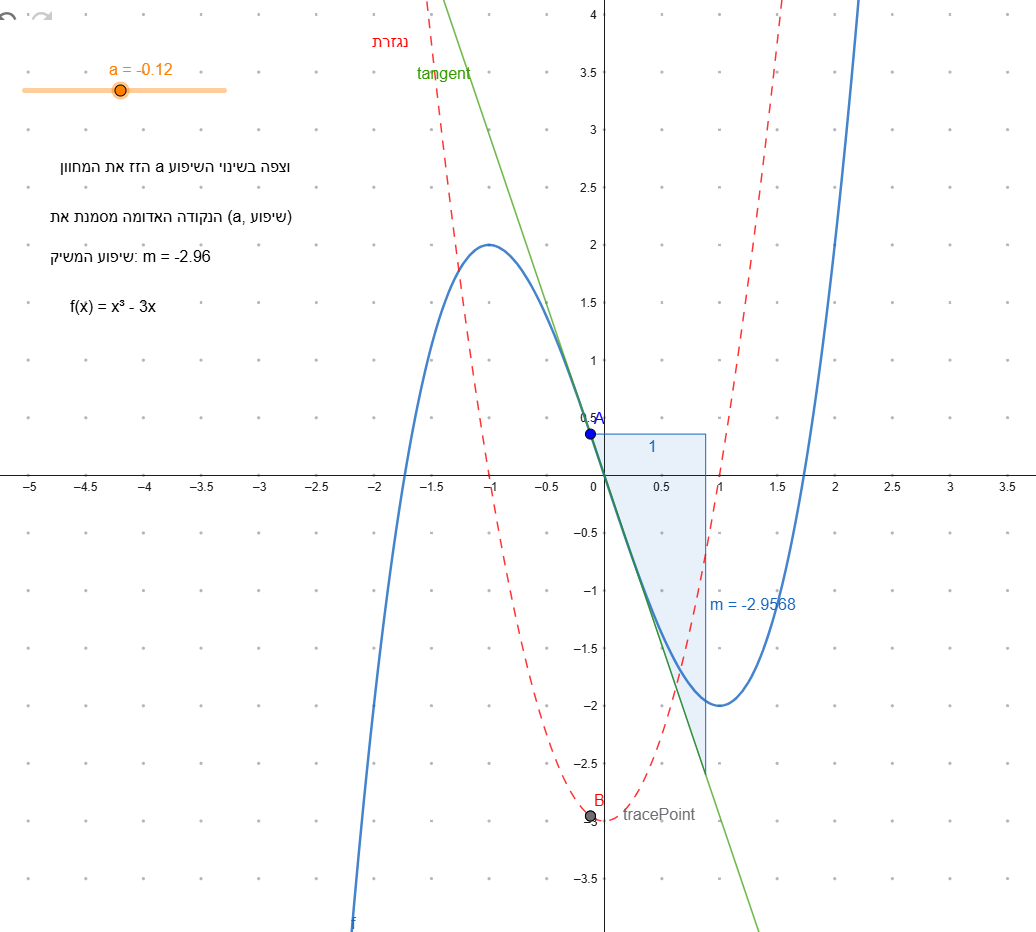
📝 משימה 1: זיהוי קעירות (פונקציה 1: f(x) = x³ - 3x)
בחרו פונקציה 1, סמנו "הצג f''(x)", והזיזו את a לאורך הגרף.
1. באיזה תחום הגרף קעור כלפי מעלה (צורת ∪)?
2. באיזה תחום הגרף קעור כלפי מטה (צורת ∩)?
3. כאשר הגרף קעור כלפי מעלה, מה סימן f''(x)?
4. היכן בדיוק נמצאת נקודת הפיתול?
5. מה קורה לגרף הסגול (f'') בנקודת הפיתול?
📝 משימה 2: שתי נקודות פיתול (פונקציה 2: f(x) = x⁴ - 4x²)
עברו לפונקציה 2 וחקרו אותה.
1. כמה נקודות פיתול יש לפונקציה זו?
2. מצאו (בערך) את ערכי x של נקודות הפיתול:
3. השלימו: בתחום שבין שתי נקודות הפיתול, הגרף קעור כלפי:
4. מה מיוחד בנקודה x = 0? (רמז: בדקו את f'' שם)
⚠️ משימה 3: הדוגמה הנגדית! (פונקציה 4: f(x) = x⁴)
🤔 שאלה חשובה: האם תמיד כש-f''(x) = 0 יש נקודת פיתול?
עברו לפונקציה 4 וחקרו אותה בעזרת הנגזרת השנייה.
1. מצאו: עבור איזה ערך x מתקיים f''(x) = 0?
2. האם בנקודה זו יש נקודת פיתול?
3. הסבירו: למה f''(0) = 0 אבל אין שם נקודת פיתול?
4. מהו התנאי המלא לנקודת פיתול?
📝 משימה 4: פונקציה מחזורית (פונקציה 3: f(x) = sin(x))
עברו לפונקציה 3 (סינוס) וצפו בהתנהגות המחזורית.
1. כל כמה מופיעה נקודת פיתול?
2. היכן נמצאות נקודות הפיתול? (רמז: איפה f'' = 0?)
3. השלימו: כאשר f = sin(x), הנגזרת השנייה היא f'' = ______
4. מדוע הגיוני שנקודות הפיתול של sin(x) הן איפה ש-sin(x) = 0?
📊 חלק ב': טבלת השוואה
מלאו את הטבלה על סמך החקירות שביצעתם:
| פונקציה | מספר נקודות פיתול | ערכי x של נקודות הפיתול | תחומי קעירות מעלה | תחומי קעירות מטה |
|---|---|---|---|---|
| f(x) = x³ - 3x | ||||
| f(x) = x⁴ - 4x² | ||||
| f(x) = sin(x) | ||||
| f(x) = x⁴ |
🏆 חלק ג': סיכום והכללה
הכללים שגילינו:
⚠️ זכרו: התנאי ההכרחי לא מספיק!
$$f''(x_0) = 0 \text{ הוא תנאי הכרחי לנקודת פיתול, אבל לא מספיק!}$$
צריך גם ש-f'' תחליף סימן בנקודה זו (ראו את הדוגמה הנגדית f(x) = x⁴).
✍️ שאלות מסכמות
1. נתונה פונקציה f כך ש: f''(x) > 0 לכל x < 2 וגם f''(x) < 0 לכל x > 2.
א) באילו תחומים הפונקציה קעורה כלפי מעלה?
ב) האם x = 2 היא נקודת פיתול? הסבירו.
2. נתון גרף של f''(x) שחותך את ציר x בנקודות x = -1 ו-x = 3.
א) כמה נקודות פיתול יש לפונקציה f (לכל היותר)?
ב) האם בהכרח יש שם נקודות פיתול? הסבירו.
🌟 אתגר למתקדמים
נתונה הפונקציה: $$f(x) = x^4 - 8x^2 + 12$$
ללא שימוש באפליקציה:
- מצאו את f''(x).
- פתרו את המשוואה f''(x) = 0.
- בדקו האם יש החלפת סימן בכל אחת מהנקודות.
- קבעו את נקודות הפיתול ואת תחומי הקעירות.
פתרון:
אחרי שתסיימו, בדקו את התשובה באפליקציה עם פונקציה מותאמת אישית!
🎉 כל הכבוד!
סיימתם את הפעילות על קעירות ונקודות פיתול.
עכשיו אתם מבינים את הקשר העמוק בין f, f' ו-f''!